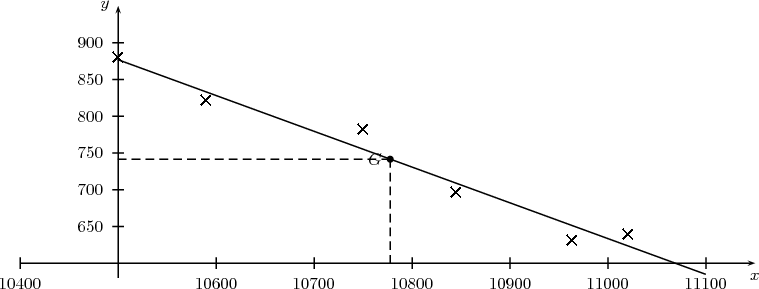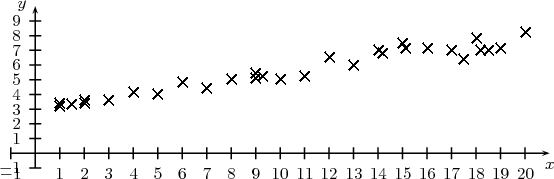
Lorsque les points du nuage paraissent presque alignés, on peut chercher une relation de la forme y = ax + b qui exprime de façon approchée y en fonction de x, autrement dit, une fonction affine f telle que l’égalité y = f(x) s’ajuste au mieux avec les données.

Graphiquement, cela signifie qu’on cherche une droite qui passe au plus près de tous les points du nuage.
Une telle relation permettrait notamment de faire des prévisions. Pour mesurer la qualité d’une telle formule, on considère, pour chaque valeur xi, la différence entre la valeur observée, c’est à dire yi, et la valeur calculée par la formule, c’est à dire axi + b. On souhaite que toutes les différences : yi - (axi + b) appelées erreurs, ou résidus, ou perturbations, soient les plus petites possible.La méthode la plus couramment employée, dite méthode des moindres carrés, consiste à choisir a et b de façon que la somme des carrés des résidus soit la plus petite possible.
On considère par la suite un nuage de points Mi(xi;yi) (avec 1 ≤ i ≤ n).

| Définition : |
| Il existe une droite unique associée au nuage Mi(xi;yi), avec i = 1,…,n telle que la somme des MiPi2 soit minimale. |
| ∙ Cette droite passe par le point moyen G(x,y) du nuage. |
∙ Elle a une équation du type y = ax + b avec a = 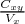 et b = y - ax. et b = y - ax. |
| ∙ Cette droite s’appelle la droite de régression de y en x. |
Utilisation de la calculatrice pour la détermination de l’équation de la droite de régression
Texas Instrument (TI - 80) :
STAT 1 : Edit … permet d’entrer les valeurs de x dans L1, puis celles de y dans L2
STAT CALC 3 : LINREG(aX+b) puis (2ndL1,2nd L2)ENTER(Ceci nous donne a et b.
Casio Graph 25
Dans le menu STAT, entrer les valeurs de x dans List 1, puis celles de y dans List 2.
, entrer dans 2VarXList : List 1 et 2VarYList : List 2
puis Calc Reg 1-Linear (On obtient alors a et b.)
Exercice : Considérons la série statistique à deux variables (xi;yi), pour i = 1,2,…,6 :
| xi | 10 500 | 10 590 | 10 750 | 10 845 | 10 963 | 11 020 |
| yi | 880 | 822 | 783 | 697 | 632 | 640 |
Solution :