3.3 Exemples d’ajustements non affines

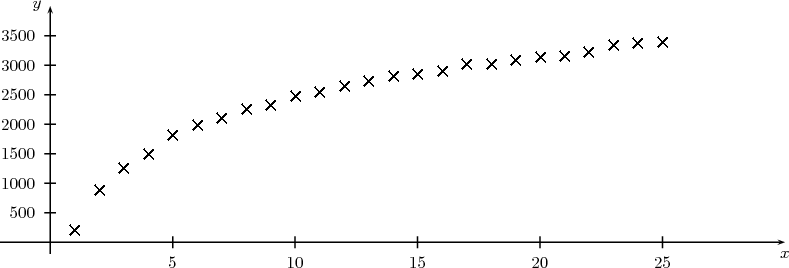
Il existe une multitude d’ajustements non affines,nous en présenterons deux des plus courants en Terminale ES.

3.3.1 Ajustement logarithmique

On considère les données suivantes :


x_i	1	2	3	4	5	6	7	8	9	10	11	12

y_i	198	881	1256	1489	1804	1983	2104	2247	2312	2468	2541	2639


x_i	13	14	15	16	17	18	19	20	21	22	23	24	25

y_i	2728	2811	2850	2890	3005	3010	3087	3125	3155	3221	3333	3365	3392

La forme du nuage ne suggère pas un ajustement affine mais éventuellelemnt un ajustement de la forme y = alnx + b

On peut le vérifier en posant t = lnx et en plaçant les points de coordonnées (t;y) dans un nouveau repère :


t_i = lnx_i	0	0,69	1,1	1,39	1,61	1,79	1,95	2,08	2,20	2,30	2,40	2,48

y_i	198	881	1256	1489	1804	1983	2104	2247	2312	2468	2541	2639


t_i = lnx_i	2,56	2,64	2,71	2,77	2,83	2,89	2,94	3	3,04	3,09	3,14	3,18	3,22

y_i	2728	2811	2850	2890	3005	3010	3087	3125	3155	3221	3333	3365	3392

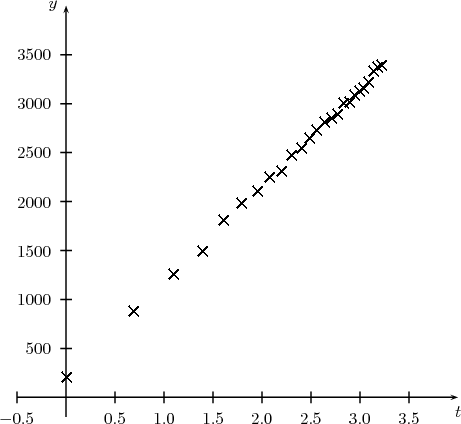
Ces points sont presque alignés, ce qui permet d’envisager un ajustement affine du type y = at + b.

Par la méthode des moindres carrées on obtient à la calculatrice a ≈ 989 et b ≈ 180 doù y = 989t + 180 (en arrondissant les coefficients à l’unité)

Comme t = lnx ,

on obtient l’ajustement logarithmique : y = 989lnx + 180 .

3.3.2 Ajustement exponentiel

On considère les données suivantes :


x_i	1	2	3	4	5	6	7	8

y_i	70	150	185	280	565	1300	3430	9100

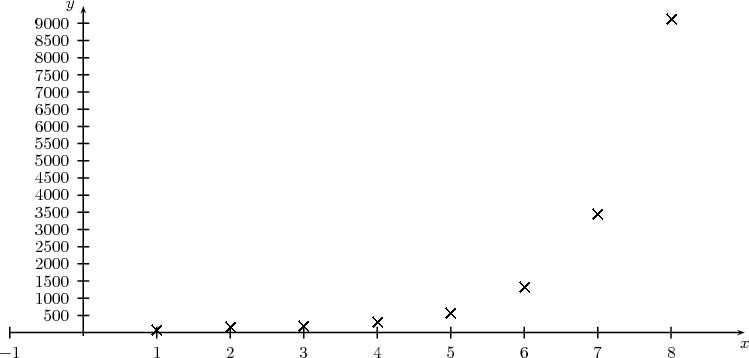
La forme du nuage ne suggère pas un ajustement affine .On pose z = lny pour obtenir des données en oronnées moins grandes.


x_i	1	2	3	4	5	6	7	8

z_i = lny_i	4,25	5,01	5,22	5,63	6,34	7,17	8,14	9,12

On place les points de coordonnées (x;z) dans un nouveau repère :

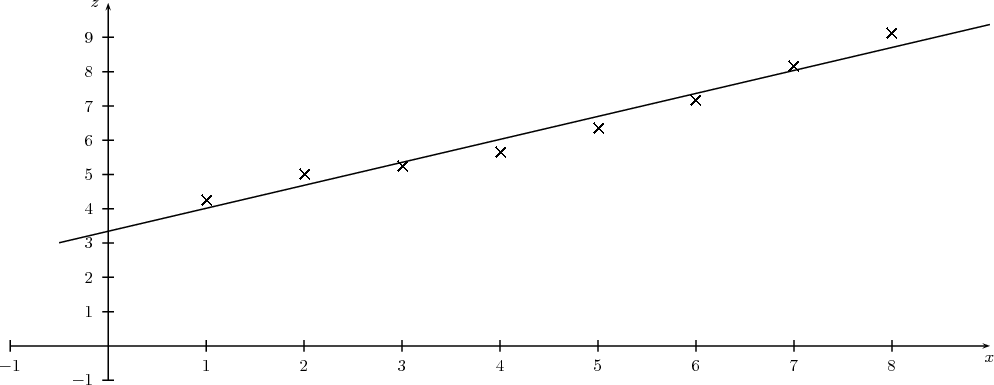
Ces points sont presque alignés, ce qui permet d’envisager un ajustement affine du type z = ax + b.

Par la méthode des moindres carrées on obtient à la calculatrice a ≈ 0,670 et b ≈ 3,344 d’ où z = 0,670x + 3,344 (en arrondissant les coefficients au millième)

Comme z = lny donc e^z = e^{ln y} donc y = e^z d’où un ajustement exponnetielle du type : y = e^0,670x+3,344 = e^0,670xe^3,344 = e^3,344e^0,670x = 28,332e^0,670x .

Ainsi

y = Ae^Bx avec A ≈ 28,332 et B ≈ 0,670.

[prec][prec-bas][début][haut]