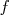[suiv][prec][prec-bas][fin][haut]

4.2 France -Septembre 2001

Sur une portion de 6 kilomètres de boulevard périphérique, le trafic peut être perturbé entre 7 h et 11 h du matin.

Au début de cette portion, un panneau indique, à chaque instant, le temps de parcours d’un véhicule sur ces 6 kilomètres.

On modélise l’évolution du trafic à l’aide de la fonction 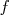f définie sur [1 ; 5] par

lnt f(t) = 8e-- +4 où e est égal à exp(1). t

Le nombre 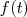f(t) est alors le temps de parcours indiqué sur le panneau et exprimé en minute, à un instant 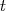t exprimé en heure. Il est 7 h du matin à l’instant t = 1 .

Le panneau indique « trafic fluide » s’il faut moins de 6 minutes pour parcourir les 6 kilomètres, Il indique « trafic perturbé » s’il faut plus de 11 minutes.

    1. Étudier les variations de f sur [1 ; 5] et dresser son tableau de variations.
    2. En déduire que le trafic n’est pas fluide à 7 h 10 min et qu’il ne l’est plus jusqu’à 11 h.
  2. Soit g la fonction définie sur [1 ; 5] par
    2 g(t) = (lnt).

    1. Calculer g′(t) et en déduire une primitive de f sur [1 ; 5].
    2. Déterminer, à une minute près, la valeur moyenne du temps nécessaire pour Parcourir les 6 kilomètres, entre 7 h et 11 h du matin.

[suiv][prec][prec-bas][début][haut]