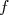 définie sur
l’intervalle
définie sur
l’intervalle ![[0 ; 6]](images/CALCUL_INTEGRAL_WEB243x.png) par :
par :
On considère la fonction 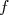 définie sur
l’intervalle
définie sur
l’intervalle ![[0 ; 6]](images/CALCUL_INTEGRAL_WEB243x.png) par :
par :
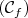 ci-contre est représentative de
la fonction
ci-contre est représentative de
la fonction  dans un repère orthonormal du
plan d’origine O.
dans un repère orthonormal du
plan d’origine O.
 , l’axe des abscisses, l’axe des
ordonn ées et la droite d’ équation
, l’axe des abscisses, l’axe des
ordonn ées et la droite d’ équation  .
.
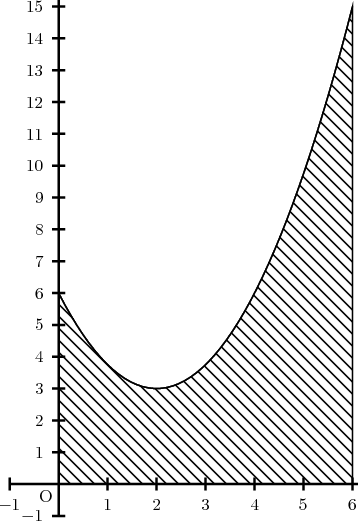
 de la partie hachurée.
de la partie hachurée.
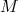 appartenant à la courbe
appartenant à la courbe 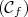 d’abscisse
d’abscisse  avec
avec ![x ∈ [0 ; 6]](images/CALCUL_INTEGRAL_WEB254x.png) .
.
La parallè le à l’axe des ordonn ées passant par 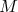 coupe l’axe des abscisses en un point
coupe l’axe des abscisses en un point 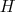 .
.
La parallè le à l’axe des abscisses passant par 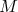 coupe l’axe des ordonn ées en un point
coupe l’axe des ordonn ées en un point 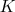 .
.
On appelle 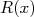 l’aire, en unit és d’aire, du rectangle O
l’aire, en unit és d’aire, du rectangle O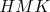 .
.
Prouver que, pour tout  appartenant à l’intervalle
appartenant à l’intervalle ![[0 ; 6]](images/CALCUL_INTEGRAL_WEB262x.png) ,
, 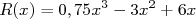 .
.
 de l’intervalle
de l’intervalle ![[0 ; 6]](images/CALCUL_INTEGRAL_WEB265x.png) telles que l’aire
telles que l’aire 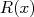 du rectangle
O
du rectangle
O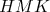 soit égale à l’aire hachur ée
soit égale à l’aire hachur ée  .
.
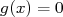 où
où 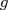 est la fonction définie
sur l’intervalle
est la fonction définie
sur l’intervalle ![[0 ; 6]](images/CALCUL_INTEGRAL_WEB271x.png) par :
par :

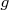 sur l’intervalle
sur l’intervalle ![[0 ; 6]](images/CALCUL_INTEGRAL_WEB274x.png) et dresser le tableau de variation de
et dresser le tableau de variation de 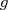 . En déduire que
l’équation
. En déduire que
l’équation 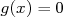 admet sur l’intervalle
admet sur l’intervalle ![[0 ; 6]](images/CALCUL_INTEGRAL_WEB277x.png) une solution unique
une solution unique 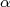 .
.
Donner une valeur approchée de 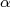 au centième.
au centième.