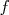une fonction impaire définie et dérivable sur ![[- 5 ; 5]](images/CALCUL_INTEGRAL_WEB195x.png)
; on désigne par 
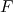une primitive de 
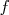sur cet
intervalle.
Chaque question comporte trois affirmations repérées par les lettres a, b, c.
Vous devez indiquer pour chacune d’elles si elle est vraie ou fausse sans justification.
Les réponses seront transcrites dans le tableau figurant en annexe.
Soit 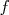une fonction impaire définie et dérivable sur ; on désigne par 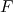une primitive d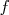e sur cet
intervalle.
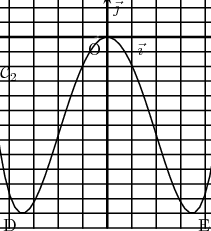
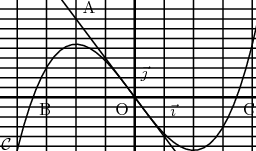
Sur les graphiques ci-dessous, le repère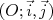 
est un repère orthogonal.
La courbe 
est la représentation graphique de la fonction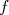 
.
Le point A a pour coordonnées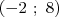 
, le point B a pour coordonnées 
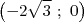et le point C a pour coordonnées
.
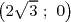La droite (OA) est la tangente en O à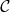 
.
1. a.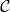 
est la courbe représentative de 
.
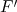b.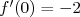 
.
c.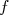 
est négative ou nulle sur ![[- 1 ; 1]](images/CALCUL_INTEGRAL_WEB209x.png)
.
2. a. Soit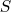 
l’aire , exprimée en unités d’aire, de la
portion de plan délimitée pu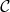 
, l’axe 
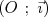et la
droite d’équation 
.
On a :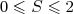 
.
b.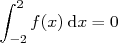 
.
c.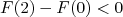 
.
3. Parmi les courbes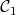 
et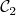 
l’une représente 
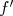et l’autre représente 
.
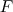a. Une équation de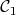 
est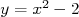 
.
b.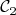 
est la courbe représentative de 
.
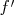c.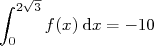 
.
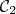est la représentation graphique d’une fonction
dérivable.
Le point D a pour abscisse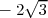 
.
Le point E a pour abscisse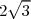 
.
