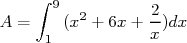Illustrons la méthode de calcul avec
Illustrons la méthode de calcul avec 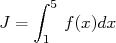 où
où 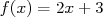 .
.
Pour calculer cette intégrale de 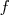 , on procède en général de la manière suivante :
, on procède en général de la manière suivante :
 on cherche une primitive
on cherche une primitive 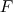 de
de 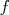 :
:
Ici 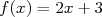 , il suffit donc de prendre
, il suffit donc de prendre 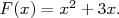
 on écrit
on écrit ![∫ 5
J = f (x)dx = [F (x)]51 = F (5) - F(1)
1](images/CALCUL_INTEGRAL_WEB60x.png)
 on réalise enfin le calcul :
on réalise enfin le calcul :
![∫ 5 ∫ 5
J = f (x)dx = (2x+ 3)dx
1 [12 ]5
= x2+ 3x 1 2
= (5 + 3× 5)- (1 + 3 ×1)
= 40- 4 = 36](images/CALCUL_INTEGRAL_WEB62x.png)
 Illustrons l’interprétation lorsque cela est possible : Remarquons que
Illustrons l’interprétation lorsque cela est possible : Remarquons que 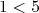 et que
et que 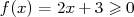 pour tout
pour tout 
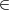
![[1;5]](images/CALCUL_INTEGRAL_WEB68x.png) .
.
Par conséquent 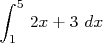 = 36 représente en u.a. l’aire du domaine
= 36 représente en u.a. l’aire du domaine  définie par
définie par 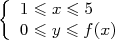
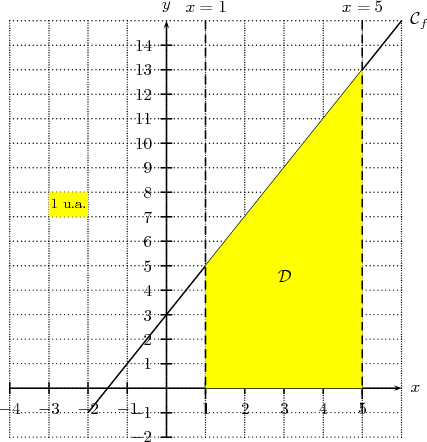
Ainsi l’aire  u.a or ici
u.a or ici  u.a.=
u.a.= 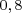 cm
cm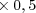 cm =
cm = 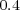 cm
cm donc l’aire vaut
donc l’aire vaut 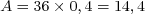 cm
cm .
.
 où
où 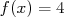
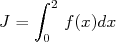 où
où 
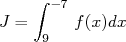 où
où 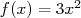
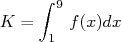 où
où 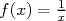
 où
où 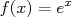
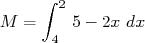
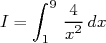 .
.