 et
et  deux réels tels que
deux réels tels que  , on note respectivement
, on note respectivement  et
et  les courbes représentatives de deux fonctions
les courbes représentatives de deux fonctions  et
et 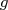 dans un repère orthogonal .
dans un repère orthogonal .
Soient  et
et  deux réels tels que
deux réels tels que  , on note respectivement
, on note respectivement  et
et  les courbes représentatives de deux fonctions
les courbes représentatives de deux fonctions  et
et 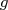 dans un repère orthogonal .
dans un repère orthogonal .
Si  et si et si  pour tout pour tout  de de ![[a;b]](images/CALCUL_INTEGRAL_WEB104x.png) ,alors ,alors  est l’aire du domaine est l’aire du domaine  ,en u.a. ,en u.a. |
Le domaine  est délimité par la courbe est délimité par la courbe 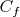 , la courbe , la courbe  et les droites d’équations et les droites d’équations  et et  . . |
EXEMPLE :
|
|
Pour des applications voir dans le livre les exercices 51-52-53 page 221