Preuve :
Soit  et
et 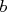 deux réels alors
deux réels alors 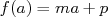 et
et 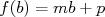 donc
donc 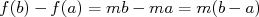 et si
et si 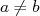 on
peut diviser par
on
peut diviser par  d’où
d’où 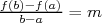 .
.
| Théorème 2 :(la réciproque) |
Soit 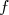 une fonction définie sur une fonction définie sur 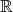 |
Si pour tout  et et 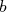 , la variation , la variation  est proportionnelle à la variation est proportionnelle à la variation  alors alors 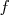 est une fonction affine. est une fonction affine. |
Autrement dit, si pour tout 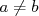 le nombre le nombre 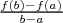 est constant alors est constant alors 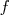 est une fonction affine dont le est une fonction affine dont le |
c÷fficient directeur est 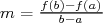 . . |
Preuve :Par hypothèse la variation  est proportionnelle à la variation
est proportionnelle à la variation  pour tout
pour tout  et
et 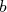 réels
.
réels
.
Notons 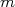 ce c÷fficient de proportionnalité donc
ce c÷fficient de proportionnalité donc 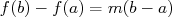 pour tout
pour tout  et
et 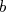 réels.
réels.
Soit  un réel quelconque , posons
un réel quelconque , posons  ,
,  alors
alors 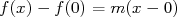 donc
donc 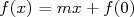 .
.
En posant 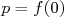 on obtient
on obtient 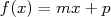 pour tout réel
pour tout réel  ,par conséquent
,par conséquent 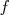 est affine.
est affine.
Exemple 1 :
Dans un repère les points  et
et 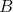 ont pour coordonnées
ont pour coordonnées 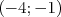 et
et 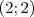 , déterminer la fonction affine représentée
par la droite
, déterminer la fonction affine représentée
par la droite 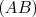 .
.
Exemple 2 :
Soit 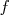 une fonction affine telle que
une fonction affine telle que 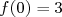 et
et 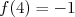 .Déterminer
.Déterminer 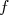 .
.