| Définition |
On appelle racines d’une fonction 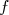 les solutions de l’équation les solutions de l’équation 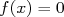 . . |
| Définition |
On appelle racines d’une fonction 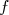 les solutions de l’équation les solutions de l’équation 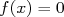 . . |
| Théorème 4 : |
Soit 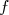 une fonction affine définie sur une fonction affine définie sur 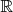 par par 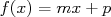 |
Si 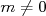 alors alors 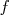 possède une unique racine égale à possède une unique racine égale à 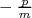 . . |
Preuve :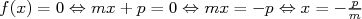 car
car 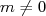 .
.
Le signe d’une fonction affine est donné,selon le signe du c÷fficient directeur 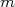 par les tableaux suivants :
par les tableaux suivants :
si 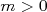 | si 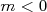 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
En résumé :
 |
|
||||||
Signe de 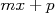 |
|
||||||