| où fi =  . . |
||||||||||||||||||||||||||||||||||||
On lance donc un dé n fois où n est un grand nombre.On obtient alors la réparttion suivante :
| Numéros de la face | 1 | 2 | 3 | 4 | 5 | 6 |
| Effectifs | n1 | n2 | n3 | n4 | n5 | n6 |
Ici la répartition des fréquences expérimentales est donc :
| où fi =  . . |
||||||||||||||||||||||||||||||||||||
La loi est équirépartie lorsque les fréquences
théoriques1
d’apparition de chacune des 6 faces valent toutes  :
:
| Numéros de la face | 1 | 2 | 3 | 4 | 5 | 6 |
| Fréquences théoriques |  |  | 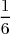 | 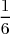 |  |  |
Pour savoir si la variation des fréquences observées d’une face à l’autre est une variation « acceptable » ,il s’agit de
déterminer si les fréquences fi sont suffisamment voisines de  .
.
Il faut donc pouvoir mesurer l’écart entre la distribution des fréquences observées et la distribution des fréquences théoriques.