2.5 Exercices

2.5.1 Exercice 1 :Extrait de l’épreuve de juin 2003

Les guichets d’une agence bancaire d’une petite ville sont ouverts au public cinq jours par semaine : les mardi, mercredi, jeudi, vendredi et samedi.

Le tableau ci-dessous donne la répartition journalière des 250 retraits d’argent liquide effectués aux guichets une certaine semaine.

On veut tester l’hypothèse :le nombre de retraits est indépendant du jour de la semaine. On suppose donc que le nombre des retraits journaliers est égal à du nombre des retraits de la semaine.

On pose d_obs² = ∑ _i=1⁵² où f _i est la fréquence des retraits du i-ème jour.

1. Calculer les fréquences des retraits pour chacun des cinq jours de la semaine.
2. Calculer alors la valeur de 1 000d_obs² (la multiplication par 1 000 permet d’obtenir un résultat plus lisible).
3. En supposant qu’il y a équiprobabilité des retraits journaliers, on a simulé 2 000 séries de 250 retraits hebdomadaires.

   Pour chaque série, on a calculé la valeur du 1000d_obs² correspondant. On a obtenu ainsi 2000 valeurs de 1000d_obs².

   Ces valeurs ont permis de construire le diagramme en boîte ci-dessous où les extrémités des "pattes " correspondent respectivement au premier décile et au neuvième décile.

   

   Lire sur le diagramme une valeur approchée du neuvième décile.

4. En argumentant soigneusement la réponse, dire si pour la série observée au début, on peut affirmer, avec un risque d’erreur inférieur à 10 %, que le nombre de retraits est indépendant du jour de la semaine ?

2.5.2 Exercice 2 :Extrait de l’épreuve de mars 2003 à Pondichéry

Un pisciculteur possède un bassin qui contient trois variétés de truites : communes, saumonées et arc-en-ciel. Il voudrait savoir s’il peut considérer que son bassin contient autant de truites de chaque variété. Pour cela il effectue, au hasard, 400 prélèvements d’une truite avec remise et obtient les résultats suivants :

1. 1. Calculer les fréquences de prélèvement f_c d’une truite commune, f_s d’une truite saumonée et f_a d’une truite arc-en-ciel. On donnera les valeurs décimales exactes.
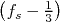   2. On pose d² = ² + ² + ².

      Calculer 400d² arrondi à 10^-2 ; on note 400d_obs² cette valeur.

      À l’aide d’un ordinateur, le pisciculteur simule le prélèvement au hasard de 400 truites suivant la loi équirépartie. Il répète 1 000 fois cette opération et calcule à chaque fois la valeur de 400d².

      Le diagramme à bandes ci-dessous représente la série des 1 000 valeurs de 400d², obtenues par simulation.

      

2. Déterminer une valeur approchée à 0,5 près par défaut, du neuvième décile D9 de cette série.
3. En argumentant soigneusement la réponse dire si on peut affirmer avec un risque d’erreur inférieur à 10 % que « le bassin contient autant de truites de chaque variété ».
4. On considère désormais que le bassin contient autant de truites de chaque variété. Quand un client se présente, il prélève au hasard une truite du bassin.

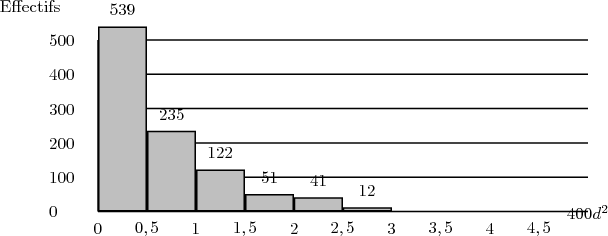
   Trois clients prélèvent chacun une truite. Le grand nombre de truites du bassin permet d’assimiler ces prélèvements à des tirages successifs avec remise.

   Calculer la probabilité qu’un seul des trois clients prélève une truite commune.