
Pour tous réels 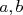 et et  de de 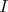 : : |
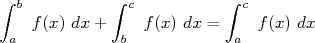 . . |
 Si
Si  et si pour tout
et si pour tout  de
de ![[a;c]](images/CALCUL_INTEGRAL_WEB187x.png) ,
, 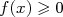 ,
,
cela signifie graphiquement que :
l’aire du domaine 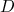 = l’aire du domaine
= l’aire du domaine 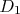 +l’aire du domaine
+l’aire du domaine 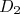 .
.
 Pour des applications voir dans le livre les exercices 55-56 page 222
Pour des applications voir dans le livre les exercices 55-56 page 222
