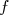 désigne une fonction continue sur un intervalle ouvert
désigne une fonction continue sur un intervalle ouvert 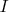 contenant deux réels
contenant deux réels  et
et 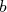 .
.
Dans toute la suite 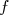 désigne une fonction continue sur un intervalle ouvert
désigne une fonction continue sur un intervalle ouvert 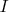 contenant deux réels
contenant deux réels  et
et 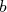 .
.
Dans le chapitre où l’on traite des primitives nous avons vu le résultat suivant :
| Théorème |
Si 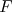 et et 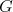 sont deux primitives de sont deux primitives de 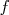 sur sur 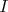 alors alors  |
On peut donc remarquer que la quantité  ne dépend pas du choix de la primitive
ne dépend pas du choix de la primitive 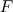 .
.
Par commodité on notera souvent ![F (b)- F (a) = [F (x)]ba](images/CALCUL_INTEGRAL_WEB11x.png) , qu’on peut lire
, qu’on peut lire 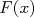 pris entre
pris entre  et
et  .
.
| Définition |
Soit 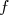 une fonction continue sur un intervalle ouvert une fonction continue sur un intervalle ouvert 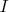 , , 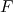 une des primitives de une des primitives de 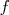 et et 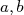 deux réels appartenant à deux réels appartenant à 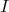 . . |
On appelle intégrale de 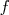 entre entre  et et 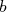 le nombre le nombre  . . |
 Ce nombre est noté : Ce nombre est noté : 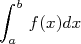 . . |
 il se lit « somme de il se lit « somme de  à à 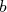 de de 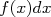 »ou « intégrale de »ou « intégrale de  à à 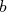 de de 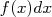 ». ». |