Exercice I :
Parmi les fonctions suivantes, quelles sont les fonctions affines ?
|
|
Exercice II :Tracer la représentation graphique de chacune des fonctions suivantes :
|
|
Exercice III :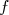 est une fonction affine. Exprimer
est une fonction affine. Exprimer 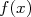 en fonction de
en fonction de  dans les cas suivants :
dans les cas suivants :
|
|
Exercice IV :
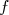 et
et 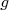 définies par
définies par 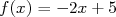 et
et 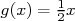
 puis
puis 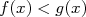 .
.
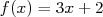 et
et 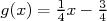
Exercice V :Dans chacun des cas suivants :
|
|
Exercice VI :
Dans un repère 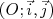 , on considère les quatre points suivants :
, on considère les quatre points suivants : 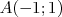 ,
, 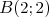 ,
, 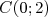 et
et 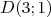
On appelle 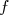 la fonction affine dont la représentation graphique est la droite
la fonction affine dont la représentation graphique est la droite 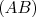 et
et 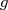 la fonction affine dont la
représentation graphique est la droite
la fonction affine dont la
représentation graphique est la droite 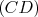 .
.
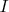 , points d’intersection de
, points d’intersection de 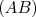 et
et
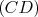 .
.
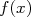 en fonction de
en fonction de  puis
puis 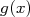 en fonction de
en fonction de  .
.
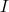 .
.Exercice VII :Voici trois tarifs de location de voiture :
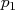 ,
, 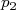 et
et 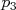 donnant le prix à payer, pour une
journée, en fonction du nombre de kilomètres parcourus.
donnant le prix à payer, pour une
journée, en fonction du nombre de kilomètres parcourus.