Dans un repère orthonormé
Exemples :  et et 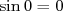 ; ;  et et 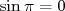 ; ;
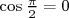 et et  |
|
|
|
| Propriété 1 |
Pour tout  réel, réel, 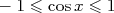 et et 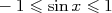 et et |
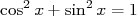 (cette dernière propriété est due au théorème de Pythagore). (cette dernière propriété est due au théorème de Pythagore). |
| Propriété 2 |
Quel que soit le réel  , , 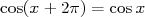 et et 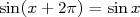 . . |
On dit que les fonctions  et et 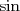 sont périodiques de période sont périodiques de période 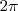 . . |
| Propriété 3 |
Quel que soit le réel  , , 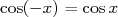 et et  . La fonction . La fonction  est paire et la fonction est paire et la fonction 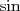 est impaire. est impaire. |