| Théorème : |
La fonction cube est croissante sur 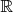 . . |
| Théorème : |
La fonction cube est croissante sur 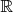 . . |
Preuve :
Soient  et
et 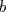 deux réels non nuls tels que
deux réels non nuls tels que 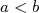 .Il s’agit de comparer
.Il s’agit de comparer 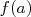 et
et 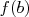 .
.
Remarquons que 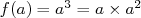 et
et 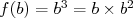 .
.
|
Etude sur
Ainsi,si
Ainsi,Si |