 dans les cas suivants :
dans les cas suivants :
EXERCICE 1 :
Encadrer  dans les cas suivants :
dans les cas suivants :
|
|
EXERCICE 2 :
Dans chaque cas représenter l’allure de la fonction inverse puis résoudre graphiquement les équations ou les inéquations suivantes :
|
|
EXERCICE 3 :
Soit 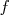 la fonction définie sur
la fonction définie sur ![]3;+ ∞ [](images/fonctions_usuelles_cours_web430x.png) par
par 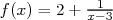 .
.
En suivant les ordres de priorités on peut décomposer le calcul de 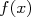 de la manière suivante :
de la manière suivante :
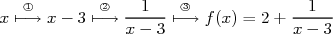
On considère deux réels  et
et 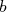 tels que
tels que 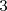 <
<  <
< 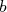 .
.
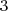 <
<  <
< 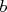 appliquer dans l’ordre chacune des 3 étapes précédentes .
appliquer dans l’ordre chacune des 3 étapes précédentes .
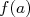 et
et  .
.
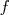 .
.EXERCICE 4 :
En appliquant la méthode précédente étudier les variations des fonctions suivantes :