| Définition |
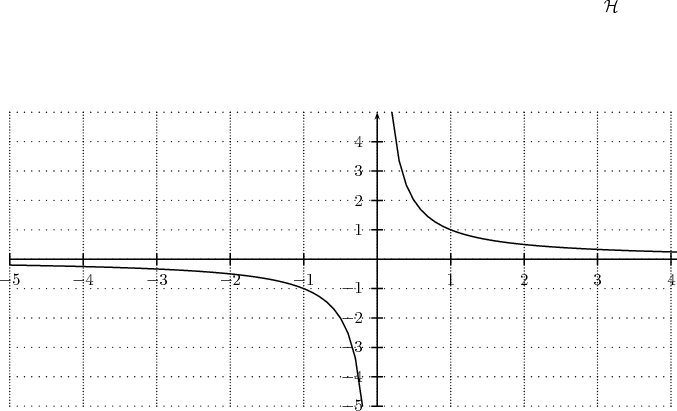
La représentation graphique de la fonction inverse est une courbe appelée hyperbole et notée 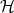 . . |
| Définition |
La représentation graphique de la fonction inverse est une courbe appelée hyperbole et notée 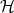 . . |
| Propriété : |
| La représentation graphique de la fonction inverse est symétrique par rapport à l’origine du repère. |
| On dit qu’elle est impaire. |
| Définition |
Soit 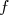 une fonction définie sur un intervalle une fonction définie sur un intervalle 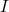 symétrique par rapport à 0. symétrique par rapport à 0. |
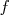 est impaire est impaire  pour tout pour tout  de de 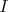 , , . . |
Preuve :
 est bien symétrique par rapport à 0. La représentation graphique d’une fonction est symétrique par rapport à origine du
repère se traduit par le fait qu’un nombre et son opposé ont des images opposées par
est bien symétrique par rapport à 0. La représentation graphique d’une fonction est symétrique par rapport à origine du
repère se traduit par le fait qu’un nombre et son opposé ont des images opposées par 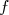 .Comparons dans le cas de la
fonction inverse
.Comparons dans le cas de la
fonction inverse  et
et 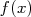 .
.
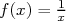 et
et  ainsi
ainsi  et
et  ont donc des images opposées par
ont donc des images opposées par 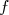 .
.
La représentation graphique de la fonction inverse est donc symétrique par rapport à l’origine du repère.