| Théorème : |
La fonction inverse est décroissante sur l’intervalle ![]- ∞; 0[](images/fonctions_usuelles_cours_web364x.png) et sur et sur ![]0;+∞ [](images/fonctions_usuelles_cours_web365x.png) . . |
| Théorème : |
La fonction inverse est décroissante sur l’intervalle ![]- ∞; 0[](images/fonctions_usuelles_cours_web364x.png) et sur et sur ![]0;+∞ [](images/fonctions_usuelles_cours_web365x.png) . . |
Preuve :
Soient  et
et  deux réels non nuls tels que
deux réels non nuls tels que 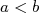 .Il s’agit de comparer
.Il s’agit de comparer  et
et 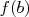 .
.
Or dans le chapitre sur l’ordre nous avons établi le résultat suivant :
Donc avec le point de vue fonctionnel :
|
Ainsi  inverse l’ordre sur
inverse l’ordre sur  et sur
et sur ![] - ∞; 0]](images/fonctions_usuelles_cours_web387x.png) .
.
 |  | 0 |  |
||
 |  |  |  | ||