[suiv][fin][haut]

1.1 Moyenne ,Médiane et écart type

1.1.1 Moyenne

Définition
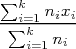On la note x et elle est définie par : x = ∑ki=1nixi -∑k---n-- i=1 i = n1x1 + n2x2 + ...+ nkxk ---n1-+-n2 +-...+-nk--

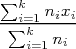n1,n2,n3,…,nk sont les effectifs correspondants aux valeurs x1,x2,x3,…,xk, si la série est discrète , ou les centres de chaque classe, si la série est continue.

1.1.2 Médiane

Définition :
La médiane Me est un paramètre de position
Il permet de couper la population étudiée en deux groupes contenant le même nombre d’individus.
Par définition 50 % de la population étudiée a des valeurs inférieure à Me et 50 % une valeur supérieure à la Me.

Ce paramètre est utile pour donner la répartition du caractère étudié.

1.1.3 Variance et écart type

Variance :
Pour calculer la variance V d’une série statistique on utilise la formule :
V = 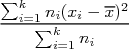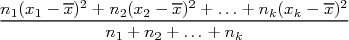∑ -- --ki=1ni(xi --x)2 ∑ki=1ni = -- -- -- n1(x1---x)2 +-n2(x2 --x)2 +-...+-nk(xk---x)2 n1 + n2 + ...+ nk

Pour calculer la variance , il faut donc calculer d’abord la moyenne.

Ecart-type
L’écart-type est le nombre noté σ tel que :σ = 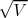√-- V

[suiv][début][haut]