| Définition |
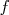 est une fonction continue sur un intervalle est une fonction continue sur un intervalle ![[a;b]](images/CALCUL_INTEGRAL_WEB134x.png) (avec (avec 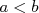 ). ). |
La valeur moyenne de  sur sur ![[a;b]](images/CALCUL_INTEGRAL_WEB137x.png) est le réel m : est le réel m : |
 |
| Définition |
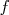 est une fonction continue sur un intervalle est une fonction continue sur un intervalle ![[a;b]](images/CALCUL_INTEGRAL_WEB134x.png) (avec (avec 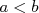 ). ). |
La valeur moyenne de  sur sur ![[a;b]](images/CALCUL_INTEGRAL_WEB137x.png) est le réel m : est le réel m : |
 |
Un exemple :
Une étude statistique a permis de modéliser par une fonction 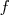 donnée ci-dessous l’évolution du nombre de personnes
âgées de plus de 85 ans, en France métropolitaine, de 1950 à 2000. On notera
donnée ci-dessous l’évolution du nombre de personnes
âgées de plus de 85 ans, en France métropolitaine, de 1950 à 2000. On notera 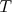 l’année. Par commodité on pose
l’année. Par commodité on pose

 désigne, en milliers, le nombre de personnes âgées de 85 ans ou plus, au 1
désigne, en milliers, le nombre de personnes âgées de 85 ans ou plus, au 1 janvier de l’année
janvier de l’année  .
.
On admet que la fonction  définie sur l’intervalle [0 ; 70] par :
définie sur l’intervalle [0 ; 70] par :  modélise de façon satisfaisante
l’évolution de cette population.
modélise de façon satisfaisante
l’évolution de cette population.
Calculer la valeur décimale approchée arrondie au millième de 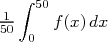 .
.
Que représente ce résultat pour la population étudiée ?
Pour des applications voir dans le livre les exercices 54- 60-61 page 223